A new way of teaching basic math?

Today, in the US education system kids are taught addition, subtraction, multiplication, division, and (for advanced students) basic algebra in Elementary School. In a way this makes sense. It provides everyone with the basic tools that they need to get through life. It lets them add times together, so they can organize their daily lives. It lets them balance a checkbook and calculate tips at restaurants.

But what if we started teaching kids advanced math concepts in elementary school? Vectors could be introduced at the same time as numbers. For example, you could teach that "5" represents 5 turtles, and [1 5] represents one turtle, and 5 apples. And that a vector like:

[1]
[5]

represents one turtle, followed by 5 turtles at another location.

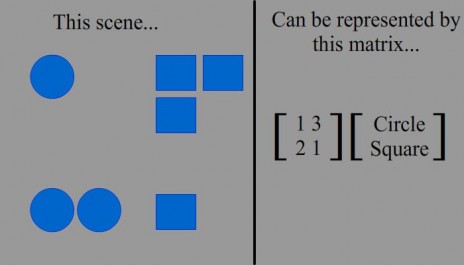
Eventually you could introduce matrices:

[1 3]
[5 7]

And could visualize it as one area with one turtle and 3 apples, and another area with 5 turtles and 7 apples.

Then when you introduce addition, you could do it for matrices, and then just say that adding single numbers is like adding two 1 X 1 matrices.

Multiplying matrices is kind of complicated, so I don't know if you could teach it in elementary school, and even if you could, I don't know if they'd understand why it works:

[1 3] X [4 2] = [1*4 + 3*8 1*2 + 3*6] = [28 20]
[5 9] [8 6] [5*4 + 9*8 5*2 + 9*6] [92 64]

But it also makes multiplication very dynamic and interesting. And it allows one to look at a matrix as a transformation, and not a data set.

A new way of teaching basic math?

Comments

Log in to Comment

mikedood 2008-12-27 14:18:22

holy christ im in high school and i have no idea wat a vector is lol. im gna go lick some bleach.

Al6200 2008-12-27 14:18:22

Yeah, they're normally not taught until college. But in the 60s there was an experiment to teach set theory (normally pretty advanced undergraduate stuff) to elementary school kids, but it didn't work too well.

Imperator 2009-01-03 17:15:41

to be honest I think kids are already being taught more advanced things earlier. I know my brother was learning things in elementary I didn't learn till HS, and things his freshman year I learned Junior year. And that's only a 4 year difference.

I like the idea of "doubling up" systems, and not just of math. The problem is of course one you've already stated: would they be able to learn all that stuff?

There's also just the problem of letting kids be kids. I think recess is just as cruicial to a kid's development as trig, but that might just be me.

Ironically the problem seems to be "solving itself" as it were; Kids might not be learning more, but adult education has and is growing by leaps and bounds, and I know more and more people heading back for Masters degrees of all types. I heard once the Masters is becoming "yesterday's" Bachelors.

Course if that's true, maybe something higher than Ph.Ds will need to be developed before long.....

Interesting stuff nonetheless.

Al6200 2009-01-03 17:15:41 (Updated 2009-01-03 22:52:14)

"to be honest I think kids are already being taught more advanced things earlier. I know my brother was learning things in elementary I didn't learn till HS, and things his freshman year I learned Junior year. And that's only a 4 year difference."

Ah. Very true. When I was in the 8th grade in middle school, there was a class of about 20 advanced kids who were learning basic algebra, and about 5 really advanced kids taking geometry.

By the time that I was a senior in high school, they had a full class taking geometry, and a few kids taking algebra 2! In 4 years my school district's math students had advanced an entire grade level (or rather, a lot of smart kids might have just moved into my town).

"I like the idea of "doubling up" systems, and not just of math. The problem is of course one you've already stated: would they be able to learn all that stuff?"

Yeah. In the 1960s, the US tried something called "New Math", where kids would be taught set theory and abstract algebra in elementary school. I don't think it worked that well though...

That said, while I think it would be interesting to teach vectors/matrices to little kids, I don't they'd end up using it much. I find it hard to believe, but there are a lot of adults who don't know what an equation is, and get by just fine.

"There's also just the problem of letting kids be kids. I think recess is just as cruicial to a kid's development as trig, but that might just be me"

Oh, definitely. Social skills are just as important as academic skills. I mean, there's no point in training someone as an engineer if they're going to become a criminal or a terrorist.

"Ironically the problem seems to be "solving itself" as it were; Kids might not be learning more, but adult education has and is growing by leaps and bounds, and I know more and more people heading back for Masters degrees of all types. I heard once the Masters is becoming "yesterday's" Bachelors."

I think that more education is a good thing, but I'm afraid that a lot of people go after the bachelors degree for the prestige, and not the for the skills/knowledge. The problem is that prestige is a negative sum game. In other words, the more people get BA's, the less prestigious the BA is. Pretty soon the masters degree might become the new "norm".

"Course if that's true, maybe something higher than Ph.Ds will need to be developed before long....."

That's a scary thought. But I bet that there are very few people who can afford to get a Ph.D. just for the prestige. Hell, I can barely afford to get a B.S. degree, and I'd like to think that it'll lead me to the career that I want.

"Interesting stuff nonetheless"

Well thanks.